Stochastische Planung für resiliente und kosteneffiziente Supply-Chains
Jul 8, 2020 • 8 min
In der Supply-Chain-Planung werden Annahmen häufig als allgemeingültige Zahlen präsentiert, obwohl eine ganze Bandbreite möglicher Resultate existiert. Eine Absatzprognose von 100 Stück sagt nicht aus, dass Sie tatsächlich exakt 100 Stück verkaufen werden. Sie besagt, dass der Verkauf auf etwa 100 Stück geschätzt wird. Manchmal auch viel mehr, manchmal viel weniger.
Die Nachfrage ist die größte Quelle von Unsicherheit in Supply-Chains – die einzige ist sie aber nicht. Lieferungen können sich verspäten, Lieferanten sind möglicherweise nicht in der Lage vollständig zu liefern, Paletten können von Gabelstaplern fallen und zerbrechen. Ein Supply-Chain-Manager beschrieb seine Arbeit einmal so: „Jeder Tag bringt eine neue Katastrophe – ich liebe es.“
Die tägliche Katastrophe zu lieben, fällt jedoch deutlich leichter, wenn man gut vorbereitet ist.
Dieses Whitepaper erklärt, wie und wann Ungewissheit in Supply-Chains mit stochastischer Planung bewältigt wird (und wann Sie darauf lieber verzichten). Im Fokus steht dabei die Unsicherheit der Nachfrage, da diese ein Problem für alle Unternehmen darstellt. Sie können die gleichen Ansätze jedoch auch für das Managen anderer Unsicherheitsfaktoren verwenden.
Was ist stochastische Planung?
Der Begriff stochastisch bezieht sich auf etwas, das nicht genau vorherzusagen ist, da es eine Zufallskomponente enthält. Stochastische Planung ist daher das Vorbereiten auf eine Reihe potenzieller Ergebnisse.
Im aktuellen „Hype Cycle for Supply Chain Planning Technologies“ verortet Gartner stochastische Supply-Chain-Planung in der Phase, die als „Abgleiten ins Tal der Enttäuschungen“ bezeichnet wird. Das bedeutet, die Analysten von Gartner rechnen damit, dass es fünf bis zehn Jahre dauern wird bis stochastische Supply-Chain-Planung signifikant zur Produktivität beitragen wird.
Wie die meisten Konzepte im Supply-Chain-Management ist auch das stochastische Planen keine neue Erfindung. Es lässt sich als ein Kontinuum betrachten, das von gängigen Praktiken bis hin zu aktuellen, von technologischem Fortschritt getriebenen Innovationen reicht. An einigen konkreten Beispielen wird dies im Folgenden veranschaulicht.
Stochastische Planung für optimale Bestände
Nimmt man Absatzprognosen als Fakt an – begegnet man also zum Beispiel einer Prognose von 100 Stück mit einer Bevorratung von exakt 100 Stück zur Erfüllung dieser erwarteten Nachfrage – würde man die Kundenbedürfnisse wohl nicht befriedigen. Selbst wenn die Absatzprognose sehr genau und die prognostizierte Menge im Durchschnitt richtig wäre, würde die Kundennachfrage doch regelmäßig nicht erfüllt werden: Ursache ist die zufällige Schwankung der Nachfrage.
Für Bestandsmanagementprofis ist das nichts Neues. Sowohl Problem als auch Abhilfe – sprich Sicherheitsbestand – sind hinreichend bekannt und Teil des Standardlehrplans des Supply-Chain-Managements. (Der gleiche Denkansatz gilt auch für Lieferzeitabweichungen – in diesem Fall ist die Lösung eine Sicherheitslieferzeit).
Ein adäquater Sicherheitsbestand schützt vor den meisten Stockouts, ohne exzessive Bestandskosten zu verursachen. Statistische Analysen sind die gängigste Art, um Sicherheitsbestände im Hinblick auf Mengen zu optimieren. Durch die Analyse des Mittelwerts und der Verteilung von Verkäufen oder Prognosefehlern kann der Pufferbestand errechnet werden, der benötigt wird, um ein Verfügbarkeitsziel von beispielsweise 98 Prozent zu erreichen. Moderne Supply-Chain-Planungssoftware berücksichtigt bei der Berechnung automatisch die Auswirkung von Losgrößen, Prüfungsintervallen und Lieferzeiten und erzielt dadurch genauere Ergebnisse.
Neue Entwicklungen im Bereich der Analysefunktionen von Software für die Supply-Chain-Planung ermöglichen jedoch eine noch präzisere Einstellung von Sicherheitsbeständen:
1. Nicht nur eine einzige Wahrscheinlichkeitsverteilung: Traditionell haben sich Berechnungen von Sicherheitsbeständen auf die Annahme gestützt, dass die Nachfrage sich normal verteilt. Insbesondere für Bestseller-Produkte erfasst die normale Verteilung (auch als Gaußsche Verteilung bekannt) Absatzmuster ziemlich genau. In manchen Situationen, speziell bei Ladenhütern, bieten andere Wahrscheinlichkeitsmaße wie etwa die negative Binomialverteilung eine bessere Passung. Neue Analysefunktionen haben es ermöglicht, bei der Optimierung von Sicherheitsbeständen andere Wahrscheinlichkeitsverteilungen zu identifizieren und anzuwenden – sogar komplett maßgeschneiderte Nachfragemodelle.
2. Dynamische Sicherheitsbestände: Im Einzelhandel variieren die Verkäufe häufig in Abhängigkeit des Wochentags. Beträgt der Absatz eines verderblichen Produkts wie beispielsweise eines Bäckerbrots montags etwa acht Stück und samstags etwa 35, sollte der Sicherheitsbestand für Montage geringer sein als für Samstage. Durch steigende Rechenleistung können nicht nur Prognosen, sondern auch Sicherheitsbestände auf Filiale-Artikel-Tagesebene verwaltet werden: So bewegen sich Sicherheitsbestände nah an der Nachfrage.
3. Bestelloptimierung nach Wahrscheinlichkeit. Die Berechnungen von Sicherheitsbeständen verwenden ein Verfügbarkeitsziel als Vorgabe. Oft lässt sich das richtige Verfügbarkeitsniveau für verschiedene Produktarten basierend auf einer Klassifikation beispielsweise nach Verkaufswert (ABC) oder Verkaufsfrequenz (XYZ) identifizieren. In manchen Fällen ist es jedoch recht komplex, die angemessenen Verfügbarkeitsziele auszumachen.
Ein gutes Beispiel hierfür ist die Dispositionsplanung von verderblichen Produkten im LEH. Selbst Produkte der gleichen Produktgruppe, wie Joghurt, können eine sehr unterschiedliche Haltbarkeit haben und damit auch ein völlig anderes Verderbsrisiko. Hinzu kommt, dass verschiedene Filialen durch unterschiedliche Größen und lokal optimierte Sortimente mehr oder weniger Ersatzprodukte im Angebot haben. Das hat eine direkte Auswirkung auf das Risiko von Stockouts und dadurch verursachte entgangene Verkäufe.
Mit mehr Rechenleistung und zunehmenden Analysefunktionen wurde es möglich, jede Nachbestellung zu optimieren und so die Gesamtkosten von Stockouts und Überbeständen basierend auf der Wahrscheinlichkeit der verschiedenen Resultate zu minimieren. Im Lebensmitteleinzelhandel bedeutet das, die Risiken von Verderb und entgangenen Verkaufsmargen auszubalancieren. Die Kostenfunktion muss dabei anpassbar sein, sodass sich einstellen lässt, wie stark sie die Regalverfügbarkeit gegenüber Verderb gewichtet: So werden einerseits die strategischen Rollen der wichtigsten Kategorien und Artikel berücksichtigt sowie andererseits die Anzahl der Möglichkeiten für eine Ersetzung, die innerhalb der Produktkategorien zur Verfügung stehen.
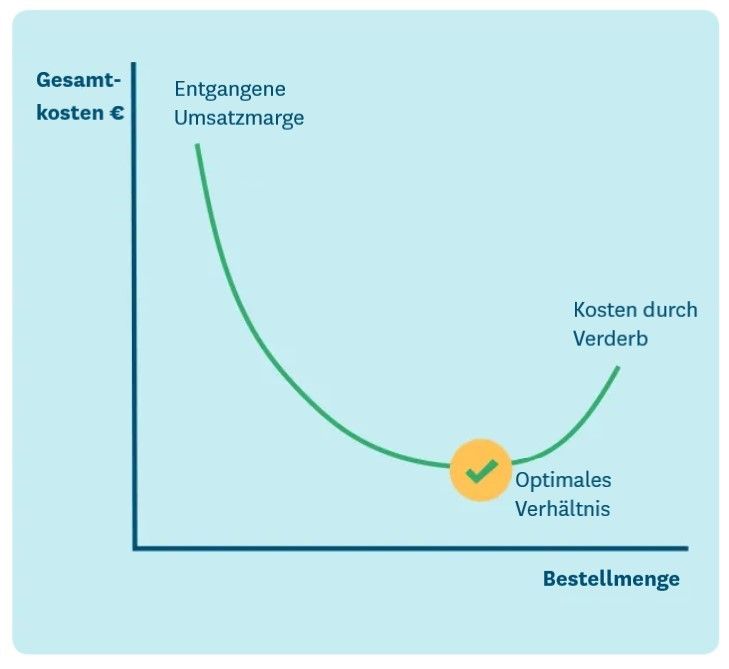
So viel Mathematik klingt kompliziert? Die gute Nachricht ist, dass alles, was Sie über die Verwendung von Sicherheitsbeständen (oder Zeit- und Kapazitätspuffern) wissen, um Sie vor Zufallsschwankungen zu schützen, weiterhin gültig ist. Neue Technologie ermöglicht es Ihnen jedoch, optimale Sicherheitsbestandsmengen zu präzisieren und einfacher zu finden.
Stochastische Planung in mehrstufigen Supply-Chains
Bei den bisher behandelten Ansätzen zum Umgang mit Nachfrageunsicherheit werden Bestände für ein Warenlager oder eine Filiale optimiert. Doch wie verhält es sich mit dem Management mehrstufiger Lieferketten, wie etwa für Verteilzentren, die Filialen beliefern?
Ein stochastisches Problem oder lediglich eine nicht integrierte Lieferkette?
Eine unangenehme Wahrheit lautet: Ein großer Teil der Unsicherheit in Supply-Chains ist selbst verschuldet.
Die Distribution im Einzelhandel ist ein gutes Beispiel: Allzu oft werden Filialdisposition und Bestandsmanagement in den Verteilzentren oder zentralen Lagern als separate Prozesse behandelt und gemanagt – und durch separate Prognosen gesteuert. Die Disponenten in den Verteilzentren wenden viel Zeit auf, abzuschätzen, wie die Filialen im Vorfeld einer anstehenden Kampagne die Bestände aufstocken, wann sie Displays saisonaler Produkte aufstellen werden und wie lange die ersten Kartons eines neuen Produkts reichen werden, bis die Filialen Nachschub benötigen.
Der Versuch, zu erraten, was die Filialen planen, ist kein Problem der Stochastik. Es ist ein Problem schlechten Supply-Chain-Managements.
Best Practice ist es, die Prognosen der Verteilzentren auf den projizierten Bestellungen der Filialen basieren zu lassen: So werden sowohl die pull-basierte Nachfrage als auch die geplanten, push-basierten Bestandsbewegungen abgebildet. In einer aktuellen Studie gaben nur 14 Prozent der befragten nordamerikanischen Lebensmitteleinzelhändler an, dies umgesetzt zu haben.
Um eine nahtlose Integration von Filial- und Distributionsplanung zu erreichen, muss das Planungssystem in der Lage sein, projizierte Filialbestellungen pro Produkt, Filiale und Tag zu berechnen, und zwar mehrere Monate oder sogar ein Jahr in die Zukunft. Darüber hinaus müssen die Berechnungen aktuelle sowie bekannte künftige Dispositionsparameter (wie etwa Sicherheitsbestände, Losgrößen und Dispositionszeitpläne), die Absatzprognosen sowie geplante Bestandsbewegungen (wie etwa das Aufstocken der Filiallager vor Produkteinführungen, Kampagnen oder Saisons) berücksichtigen. Diese Berechnungen sind machbar, erfordern jedoch bedeutende Datenverarbeitungskapazitäten – was wahrscheinlich ein Grund für die erstaunlich niedrige Aneignungsrate ist.
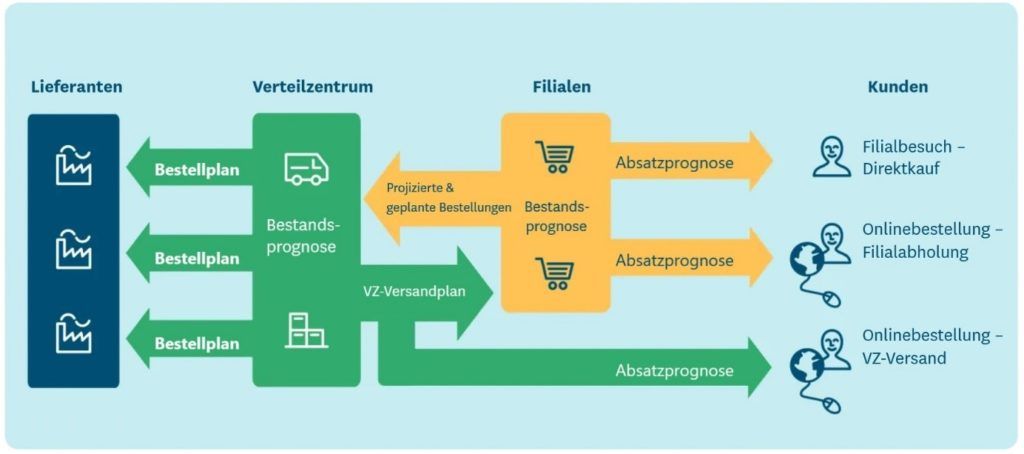
Der gleiche Ansatz lässt sich selbstverständlich auch in Bezug auf die Verfügbarkeit bei vorgelagerten Lieferanten anwenden: Diese erhalten nicht nur Zugang zu den geschätzten jährlichen Abnahmemengen, sondern auch zu den aktuellen Projektionen der Bestellaufträge.
Stochastische Planung für Langsamdreher
Werden projizierte Bestellungen über die Filialen hinweg aggregiert, bilden sie eine sehr akkurate, kundengesteuerte Prognose für die Verteilzentren, die die Filialen versorgen. Bei sehr langsam drehenden Produkten kann dieser Ansatz jedoch in der vorgelagerten Prognose eine systematische Verzerrung einbringen.
Das Problem der Verzerrung kann mit stochastischem Planen gelöst werden.
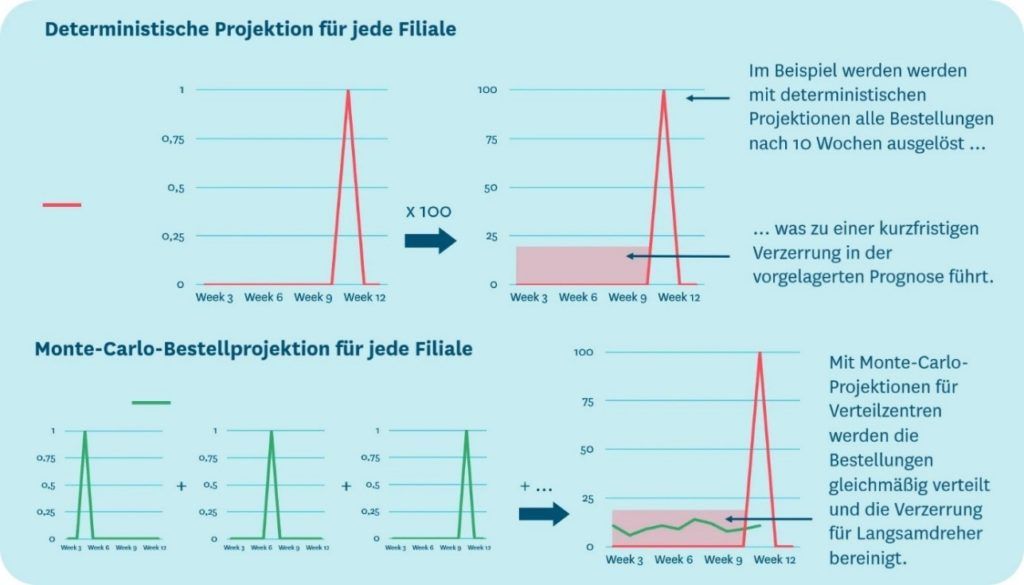
Ein Beispiel: Im Durchschnitt verkaufen sich pro Woche 0,1 Einheiten eines Langsamdrehers. Verkauft die Filiale eine Einheit mehr des Produkts, sinkt deren Bestandsmenge tief genug, um eine Auffüllbestellung auszulösen. Auf Grundlage der Prognose wird projiziert, dass diese Bestellung in zehn Wochen ab dem jetzigen Zeitpunkt stattfindet. Da die Nachfrage nach dem Langsamdreher im Wesentlichen zufällig ist, ist die Wahrscheinlichkeit, dass die Filialen diese bestellauslösende Einheit nächste Woche, in drei Wochen oder in zehn Wochen verkaufen, gleich hoch. Daraus leitet sich ab, dass die projizierten Bestellungen, insbesondere wenn sie über mehrere Filialen mit ähnlichen Absatzmustern aggregiert werden, die kurzfristige Nachfrage für Langsamdreher systematisch unterschätzen.
Ein Modellierungsansatz ist die Monte-Carlo-Simulation: Sie kann zur gleichmäßigen zeitlichen Verteilung der projizierten Auffüllbestellungen von langsam drehenden Produkten verwendet werden. Für die einzelne Filiale ergibt sich daraus kein Unterschied – die Filiale muss weiterhin die gleiche Menge des Sicherheitsbestands führen, um die Verfügbarkeit zu gewährleisten. Auf Ebene der Verteilzentren wird die Prognosegenauigkeit von Langsamdrehern jedoch signifikant verbessert.
Wann ist stochastische Planung nicht anwendbar?
Bisher betrachteten wir die alltägliche Unsicherheit, die durch Zufallsschwankungen in der Nachfrage oder bei Prozessen verursacht wird. Wie verhält es sich jedoch mit echten Katastrophen wie verheerenden Wirbelstürmen, Streiks oder abgebrannten Produktionsanlagen?
Die kurze Antwort lautet, dass stochastische Planung für diese Art von einmaligen Ausnahmefällen nicht anzuwenden ist.
Stochastische Planung basiert auf Wahrscheinlichkeitsverteilungen. Um diese nutzen zu können und daraus die Wahrscheinlichkeit verschiedener Ergebnisse zu modellieren, muss eine große Datenmenge verfügbar sein: beispielsweise historische Verkaufsdaten, Liefer- oder Herstellungsdaten. Solche Erfahrungswerte aus der Vergangenheit stehen glücklicherweise für wirklich große Katastrophen nicht zur Verfügung.
Es gibt jedoch andere Ansätze, wie etwa Szenarienplanung, die auf digitalen Zwillingen basiert: Mit ihr lassen sich verschiedene Szenarien vergleichen, wie etwa ein Wirbelsturm, der eine Stadt mit mehreren unterschiedlichen Schweregraden trifft. Anhand des digitalen Zwillingsmodells lassen sich Ermessensentscheidungen darüber treffen, wie die Vorbereitung auf mögliche Desaster oder das geeignetste Vorgehen in einer kritischen Situation aussehen sollte.
Das Problem zu verstehen ist wichtiger als raffinierte Rechenmethoden
Die Modellierung macht Spaß und je fortgeschrittener die Mathematik, desto eindrucksvoller die Lösung – stimmt’s?
Doch bevor Sie angesichts der Wahrscheinlichkeitsverteilungen in Begeisterung ausbrechen und Ihre eingestaubten Statistiklehrbücher hervorkramen, sollen hier noch einmal einige Punkte der vorherigen Abschnitte wiederholt werden:
1. Nicht alle Unsicherheitsprobleme von Supply-Chains eignen sich für stochastische Planung.
- Manchmal muss der Supply-Chain-Prozess angepasst werden, statt fortgeschrittene Modellierung auf eine Unsicherheit anzuwenden, die durch eine nicht integrierte Supply-Chain verursacht wird.
- Stochastische Planung lässt sich auf Prozesse anwenden, für die historische Daten vorliegen, wie etwa Verbrauchernachfrage oder Herstellungsprozesse. Eine niedergebrannte Produktionsstätte sollte nicht in diese Kategorie fallen.
2. Stochastische Planung klingt ausgefallen, bezeichnet im Grunde aber die probate Praxis, Bestands-, Zeit und Kapazitätspuffer zu verwenden (je nachdem, was in einer bestimmten Situation am sinnvollsten ist), um die Auswirkungen von Zufallsschwankungen zu mindern.
- Fortgeschrittene Mathematik macht dieses Puffern lediglich effektiver.
Quellen:
Hype Cycle for Supply Chain Planning Technologies by Gartner, 2017
Verlieren Sie Zeit und Geld, weil Ihre Supply-Chain schlecht integriert ist?
Erfolgreich im LEH: Best Practices für das Managen von Supply-Chains im Lebensmitteleinzelhandel




